Andregradsligning
En andregradsligning, annengradsligning eller kvadratisk ligning, er en matematisk ligning på formen


Ligningen har tre koeffisienter , og samt en ukjent , som alle representerer reelle eller komplekse tall. Generelt har ligningen to løsninger, også kalt røtter.
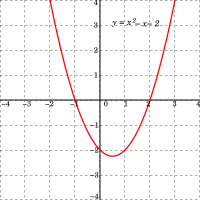
Venstre side i ligningen er polynomfunksjonen , som i det reelle tilfellet grafisk fremstiller en parabel. Røttene i andregradsligningen er lik nullpunktene til andregradspolynomet, det vil si de verdiene av som gir . Ligningen kan ha to, én eller ingen reelle røtter, avhengig av om funksjonen skjærer, tangerer eller ligger helt over eller under -aksen.
Røttene i andregradsligningen kan uttrykkes ved hjelp av den såkalte ABC-formelen.
ABC-formelen
redigerDe to røttene til andregradsligningen kan skrives på formen
hvor symbolet «±» indikerer at det eksisterer to løsninger:
-
- og
Uttrykket under kvadratroten, , kalles diskriminanten . En ligning med reelle koeffisienter vil få to reelle røtter når diskriminanten er positiv , to reelle sammenfallende røtter når diskriminanten er null og to kompleks konjungerte røtter når diskriminanten er negativ :
og
og
ABC-formelen kan også skrives som:
som kan forenkles til:
Denne formen egner seg godt når man bruker en kalkulator med kvadratrot-funksjon og én minneplass eller flere for å finne røttene til andregradsligninger. Uttrykket under kvadratroten er en diskriminant. Formen over passer også godt når komplekse røtter kan godtaes. Da vil uttrykket utenfor kvadratroten være den reelle delen og kvadratrot-uttrykket være den imaginære delen:
Ved hjelp av ligningens røtter kan andregradspolynomet faktoriseres på formen
Alternativ formel for løsningen
redigerHvis koeffisienten , så kan løsningene av andregradsligningen skrives på den alternative formen
Merk at hvis , så gir denne formen den ene korrekte løsningen, , men ikke den andre løsningen,
Viètes formler
redigerViètes formler gir en enkel sammenheng mellom røttene til en polynomligning og koeffisientene i ligningen. For andregradsligningen har formlene formen
Herav følger at:
- og
Når koeffisientene og røttene i andregradsligningen er relle, kan Vietes formler brukes for å beregne ekstremalverdien for polynomfunksjonen , det vil si maksimal- eller minimalverdien til funksjonen. Fra grafen til andregradspolynomet kan man i dette tilfellet se at ekstremalverdien gitt for et argument ligger midtveis mellom de to røttene. Fra Vietes første formel finner man
Ekstremalverdien finner man da ved innsetting i funksjonen
Eksempler
rediger| Andregradsligning | Diskriminant | Røtter | |
|---|---|---|---|
| To reelle røtter. | | ||
| To reelle sammen- fallende røtter. |
|||
| To kompleks konjungerte røtter. |
| ||
Anvendelse på ligninger av høyere grad
redigerI enkelte tilfeller kan en høyere grads ligning løses ved å innføre en variabelsubstitusjon som reduserer problemet til en andregradsligning. Et eksempel er ligningen
som ved hjelp av substitusjonen reduseres til
Denne ligningen lar seg lett løse for ved hjelp av ABC-formelen som gir to reelle røtter: og Dette fører videre til at
- og
Utledning av ABC-formelen
redigerMultipliserer man den opprinnelige andregradsligningen med koeffisienten , får den denne formen
Ligningen blir lettere å arbeide med ved å innføre en ny variabel ,
Leddene som inneholder kan gjøres om til et fullstendig kvadrat ved å legge til et ledd på begge sider av likhetstegnet, samtidig som man flytter leddet over på høyre side av ligningen:
Ved hjelp av første kvadratsetning kan venstre side nå skrives som et fullstendig kvadrat:
Denne enkle andregradsligningen har to røtter, gitt ved
En liten omforming gir
Siden gir dette ABC-formelen.
Historie
redigerAndregradsligninger opptrer i mange praktiske problemer relatert til arealberegninger, og det er derfor ikke uventet at slike ligninger har en lang historie i matematikken. Problemer der andregradsligningen opptrer har vært viktig for forståelsen av tall og begreper som rasjonale, irrasjonale og komplekse tall.
På babylonske leirtavler, datert mellom 1800 og 1600 f.Kr., finner man mange referanser til slike problemer, f.eks: Finn lengden til et kvadrat der areal minus sidelengde er lik 870. Både problemstilling og løsningsmetode er beskrevet med ord, men i dagens symbolform er dette ekvivalent til løsningen av ligningen
Den beskrevne løsningsmetoden svarer også til bruk av den positive roten i ABC-formelen, og den korrekte løsningen: er oppgitt.
Det skulle gå svært lang tid før det ble akseptert at andregradsligningen også kunne ha negative røtter. Helt frem til middelalderen konsentrerte studiet av andregradsligninger seg om de tre formene som kan ha en positiv rot:
der og er ikke-negative tall. Man finner eksempler på alle disse tre typene i de babylonske tekstene.
Problemer der koeffisienten løste babylonerne ved å innføre en substitusjonen som overførte det opprinnelige problemet til et ekvivalent problem for med første koeffisienten lik . Med kjennskap til moderne symbolform for ligningen er dette i dag enkelt, men det vitner om betydelig matematisk innsikt når babylonerne kunne gjøre dette basert på en tekstbeskrivelse av ligning og løsning. Babylonerne løste også høyeregradsligninger ved å bruke substitusjon for å redusere problemet til en andregradsligning.
Egyptisk matematikk nådde ikke like høyt som den babylonske, og løsning av andregradsligninger med tre koeffisienter var ukjent for de gamle egypterne.
I den tiende delen av læreverket Elementer ga den greske matematikeren Evklid, som levde omtrent 300 år f.Kr., en geometrisk metode for løsning av andregradsligningen på formen iii). Han drøftet også vilkårene for at koeffisienten skal være kommensurabel med rotdelen av løsningen, dvs. at brøken
- er et rasjonalt tall.
Den greske matematikeren Diofant levde omtrent 500 år senere, og i verket Arithmetica var han den første til å innføre en synkopert algebra med en slags symbolnotasjon for ligninger. Ved hjelp av symboler for den ukjente, for ulike potenser av denne og for koeffisientene, skrev han både andregradsligninger og høyeregrads ligninger på kompakt form. For andregradsligninger ga Diofant bare den største roten, negative røtter ble ikke akseptert.
Den første matematikeren som oppga negative røtter til andregradsligningen var Brahmagupta, som levde i det sentrale India i det 7. århundre. På samme måte som Diofantes brukte Brahmagupta en slags symbolnotasjon for ligninger.
Vel 150 år senere, i det 9. århundre, skrev araberen Muhammad ibn Musa al-Khwârizmî verket Al-jabr wa’l muqabalah som inneholdt en oversikt over løsning av alle typer andregradsligninger med positive røtter. I tilfeller med to positive røtter er begge oppgitt. Også betydningen av fortegnet til diskriminanten er omtalt. Navnet algebra er en omforming av første ordet al-jabr i tittelen på dette viktige verket, som innførte en ny systematikk i studiet av ligninger.
Et manuskript etter den tyrkiske matematikeren abd-al Hamid ibn-Turk inneholder mye av det samme materiale som i Al-jabr. Manuskriptet er skrevet omtrent samtidig med det arabiske manuskriptet, og det har derfor vært reist spørsmål om hvilket verk som kom først og om det ene bygger på det andre.
En rekke manuskripter fra det 11. og det 12. århundre viser at kinesiske matematikere brukte metoder tilsvarende det som i dag kalles Horners regel for å finne approksimative røtter til polynomligninger av helt opp til fjortende grad.
Franskmannen François Viète (1540 – 1603) videreutviklet notasjonen for ligninger og innførte bruk av symboler også for koeffisientene. Symbolene og for addisjon og subtraksjon var allerede i bruk, men Viète tok i bruk en vokal som symbol for den ukjente og konsonanter , , … for koeffisientene. Symbolbruken var likevel ikke helt gjennomført, da ble betegnet , multiplikasjon ble markert med det latinske ordet og likhetsrelasjonen ble markert med ordet . Den generelle formen for andregradsligningen kunne dermed skrives
- B in A quadratus + C in A aequalis D.
Viète utviklet også relasjoner mellom de ukjente og koeffisientene for de tilfeller der alle størrelsene er positive tall.
René Descartes' arbeid La geometrie er en av de tidligste matematiske tekstene som omhandler algebra som er mulig å følge i dag, uten å ha vansker med notasjonen. Dette ble publisert i 1637, som et appendiks til det større verket Om metoden. Det første bindet i appendikset inneholder en drøfting av løsning av andregradsligninger ved hjelp av en geometrisk konstruksjon. Som så mange før ham, neglisjerte Descartes i dette bindet negative løsninger. I det tredje bindet av La geometrie finnes en mer generell drøfting av løsning av algebraiske ligninger.
Først med teorien for komplekse tall, utviklet av blant andre Abraham de Moivre, Leonhard Euler og Carl Friedrich Gauss, fikk løsningen av andregradsligningen en komplett beskrivelse.
Se også
redigerLitteratur
rediger- C.B.Boyer: A history of mathematics. John Wiley & Sons, Inc, 1968, ISBN 0-691-02391-3
Eksterne lenker
rediger- Kalkulator for å finne røtter i andregradslikninger, hos Kalkuler.no
- «Løs en andregradslikning», fra matematikk.org
- «Andregradslikninger», fra matematikk.net











