Sirkelens kvadratur
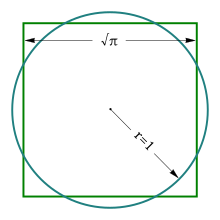
Sirkelens kvadratur er et klassisk problem i geometri som består i å bestemme sidelinjen i et kvadrat som har samme areal som innenfor en sirkel kun ved bruk av passer og linjal. Hvis radius i sirkelen er r = 1, er svaret gitt som kvadratroten av π. Løsningen av problemet er derfor ekvivalent til å bestemme den numeriske verdien π = 3,1415926536... av denne konstanten ved en geometrisk konstruksjon som ikke tillater andre hjelpemidler enn passer og linjal.
Spesielt greske matematikere i antikkens Hellas var opptatt med dette problemet og la stor vekt på å finne en løsning, uten å lykkes. I stedet ble det utviklet et stort antall approksimative løsninger som ga stadig mer nøyaktige verdier for tallet π. Slik fortsatte problemet å bestå frem til 1882 da den tyske matematiker Ferdinand von Lindemann viste at π er et transcendentalt tall som er umulig å bestemme ved en ren geometrisk konstruksjon.
På tross av dette har likevel mange i ettertid fortsatt å søke etter en slik løsning med et skjult håp om at det likevel skal la seg gjøre. Å være opptatt med sirkelens kvadratur i dag er derfor synonymt med å kaste bort tid og krefter på en umulig oppgave.
Babylonsk matematikk
redigerI det gamle Mesopotamia 1000-2000 år f.Kr. var det tilsynelatende lite interesse for geometriske problem. I praksis synes de å ha brukt verdien π = 3. Dette er også en verdi som er omtalt i Første Kongebok (7:23) i Bibelen om kong Salomo som lot bygge et rundt kar for sitt tempel. Det skulle ha en diameter på 10 og omkrets 30 med datidens lengdeenheter.
Men på en steintavle fra den tiden er tallet 24/25 funnet sammen med en tegning av en sekskant innskrevet i en sirkel. Nå er omkretsen av sekskanten tre ganger så stor som diameteren i sirkelen. Så hvis tallet 24/25 er forholdet mellom omkretsene til sekskanten og sirkelen, gir det at π = 25/8 = 3 + 1/8 = 3,125. Denne mer nøyaktige verdien er mer spekulativ og har tilsynelatende hatt liten betydning.[1]
Det gamle Egypt
redigerDen beste kjennskapen til matematikk i det gamle Egypt er kommet fra den såkalte Rhind-papyrusen som stammer fra ca. år 1600 f.Kr. Den inneholder en samling av matematiske problemer med løsninger. Herav går det frem at arealet innen en sirkel tilsvarer et kvadrat med sidelengde som er diameteren til sirkelen redusert med en niendedel. Hvis diameteren kalles d, må man derfor ha at π(d/2)2 = (d - d/9)2 som betyr at π = (4/3)4 = 256/81 = 3 + 1/9 + 1/27 + 1/81 = 3,160... . I praktisk arbeid ser det ut til at man i stedet kan ha brukt verdien π = 22/7 = 3 + 1/7 = 3,143... som også er mer nøyaktig. Denne ble iallfall ofte benyttet i dagliglivet i senere århundre opp til moderne tid.
Antikkens Hellas
redigerDen første greske naturfilosof man kjenner til og som var opptatt av arealet til en sirkel, er Anaxagoras. I en historie om hans virke, blir det sagt at han gjorde dette i en periode han måtte sitte i fengsel. Ingen konkret, ny innsikt resulterte fra dette.
Derimot gå arbeidene til Hippokrates fra Khíos håp om å kunne gjennomføre denne beregningen. Han oppdaget at visse deler av sirkelflaten kunne beregnes eller konstrueres. Disse så ut som sigder og blir nå kalt for luner da formen minner som halvmåner. Dette kunne bety at hele sirkelflaten kunne beregnes. Han kunne til og med vise at sirkelflaten pluss arealet til en lune var like stort som et kvadrat. Men det ble raskt klart at akkurat denne lunen ikke kunne la seg konstruere.
I Euklids store verk Elementer om geometri, blir ikke problemet med sirkelens kvadratur omtalt. Men han gir et bevis for at arealet til sirkelen er proporsjonalt med kvadratet av diameteren.
Hvis man tillot andre hjelpemidler enn kun passer og linjal, viste det seg snart at problemet kunne løses. Den første som klarte det, var den greske matematiker Dinostratos. Han var bror til Menaikhmos og begge hadde vært elever av Platon. Dette klarte han ved å ta i bruk en helt ny kurve som siden har fått navnet kvadratrisen. Men da denne ikke lot seg konstruere med passer og linjal alene, ble denne løsningen ikke ansett som tilfredsstillende.
Arkimedes
redigerDerimot var det den store matematiker Arkimedes som ga den første, systematiske beregning av sirkelens areal basert på geometriske metoder. Han benyttet at en sirkel er tilnærmet en regulær mangekant med et stort antall sidekanter. En nedre grense for omkretsen til sirkelen kunne han da finne ved å innskrive slike polygoner, mens en øvre grense kom frem ved å benytte omskrevne polygoner. Han startet med en regulær 6-kant, en heksagon. Har sirkelen radius r = 1, vil dette også være sidekanten i den innskrevne heksagonen som derved får en omkrets på 6. På den måten kommer den nedre grensen π > 3 frem. Tilsvarende vil den omskrevne heksagonen ha omkretsen 4√3 som gir den øvre grensen π < 2√3 = 3,46.. .
Med dette utgangspunktet gjentok han så beregningen med en innskrevet og omskrevet 12-kant og fikk dermed mer nøyaktig grenser. Slik fortsatte han med å dobble antall sidekanter og sa seg fornøydd etter å benyttet 96-kanter. Denne fremgangsmåten har i ettertid fått navnet utfyllingsmetoden. Resultatet han da kom frem til, var at 223/71 < π < 22/7 eller 3 + 11/71 < π < 3 +1/7 som betyr at 3,1408 < π < 3,1429. Det er en meget god tilnærming til den eksakte verdien og er et av de mest imponerende matematiske resultat fra det antikke Hellas.[2]
Hvis man benytter den senere utviklete trigonometri, kan omkretsen til en regulær n-kant yttrykkes meget kompakt. Den innskrevne mangekanten har omkrets pn = 2n sin(π /n), mens den omskrevne n-kanten har omkrets Pn = 2n tan(π /n). Begge disse uttrykkene nærmer seg 2π når antall sider n blir veldig stort. Metoden til Arkimedes med dobling av sidetallet tilsvarte da i praksis å regne ut sinus og tangens til den halverte vinkelen. Men formler for dette fantes ikke på hans tid slik at han hadde primært kun Pythagoras' læresetning å benytte.
François Viète
redigerI de følgende århundrene ble Arkimedes' metode benyttet til å gi stadig mer presise verdier for π. En ny epoke startet med den franske matematiker François Viète som på mange måter la grunnlaget for den moderne formulering av matematiske uttrykk. For første gang lykkes han i å utlede en formel som i prinsippet kan gi et så nøyaktig resultat for π som man måtte ønske. Han fant at
og benyttet dette til å beregne π med ni desimalers nøyaktighet.
Han brukte metoden til Arkimedes med å betrakte en tilnærmelse til sirkelen bestående av en serie med regulære mangekanter hvor sidetallet i hver ble fordoblet i forhold til det foregående. I stedet for å benytte omkretsen av disse, brukte Viète arealene deres. Med moderne notasjon kan arealet av den innskrevne n-kanten skrives som an = n sin(π /n)⋅cos(π /n), mens den omskrevne n-kanten har areal An = n sin(π /n)/cos(π /n). Begge disse uttrykkende nærmer seg arealet π for sirkelen når n blir veldig stor.
Viète started med å innskrive et kvadrat i sirkelen. Det har arealet a4 = 2. Forholdet mellom dette og sirkelens areal er derfor 2/π . Han skriver så dette som
Når n blir veldig stor, vil den siste faktoren an/π her bli lik 1. Man står da igjen med å regne ut produktet av alle de forangående faktorene. Dermed kan dette uttrykket skrives om på formen
hvor hver faktor er forholdet mellom arealene til to påfølgene mangekanter. Fra formelen an = (n/2) sin(2π /n) for arealet til den innskrevne n-kanten, følger da at ui = 2 cosθ uttrykt ved vinkelen θ som hver gang blir halvert. Ved å bruke formelen 2 cosθ = √(2 + 2 cos 2θ) fra trigonometrien, har man derfor at ui = √(2 + ui -1). Dette er en rekursiv relasjon som kan brukes til å beregne alle disse faktorene ut fra den første u1 = 2⋅(a4/a8) = √2. Innsatt gir dette Viètes formel.
Nyere tid
redigerI årene som fulgte ble det utviklet en mengde ny resultat for π, uttrykt både som uendelige produkt og uendelige summer. Men ingen av disse lot seg konstruere rent geometrisk. På den måten forble problemet med sirkelens kvadratur uløst frem til 1882 da den tyske matematiker Ferdinand von Lindemann viste at dette er umulig.
Likevel var den geniale, indiske matematiker Srinivasa Ramanujan i begynnelsen av forrige århundre fremdeles opptatt av problemet og viste i 1914 hvordan π kunne konstrueres ved bruk av passer og linjal med en nøyaktighet som tilsvarer åtte riktige desimaler. Men likevel var interessen for dette problemet ikke lenger så stor og heller rettet mot mer numeriske metoder basert på bruk av elektroniske regnemaskiner.
I 2020, Espen Gaarder Haug, professor i finans ved Handelshøyskolen ved NMBU og en selvlært fysiker, presenterte en praktisk måte å sirkelens kvadratur ved hjelp av relativistiske effekter (påkalle ideen om å løse problemet i det hyperbolske planet).[3]
Referanser
rediger- ^ A. Holme, Matematikkens historie, Bind 1, Fagbokforlaget, Bergen (2002). ISBN 82-7674-678-0.
- ^ C.B. Boyer, A History of Mathematics, Princeton University Press, New Jersey (1985). ISBN 0-691-02391-3.
- ^ Haug, Espen Gaarder (2020). «Squaring the Circle and Doubling the Cube in Space-Time». The Mathematics Enthusiast. 18 (1-2).
Se også
redigerLitteratur
rediger- V. Brun, Alt er tall, Universitetsforlaget, Oslo (1994). ISBN 82-13-00151-6.
- A. Holme, Matematikkens historie, vol. 1, Fagbokforlaget, Bergen (2002). ISBN 82-7674-678-0.
- S. Thorvaldsen, Matematisk kulturhistorie, Eureka Forlag, Høgskolen i Tromsø, Tromsø (2003). ISBN 82-7389-045-7.
- C. B. Boyer, A History of Mathematics, Princeton University Press, New Jersey (1985). ISBN 0-691-02391-3.
- P. Beckmann, A History of Pi, Golem Press, Boulder, Colorado (1982). ISBN 0-911762-18-3.
Eksterne lenker
rediger- MacTutor, Squaring the circle, University of St. Andrews, Scotland.
- Archimedes Estimate of Pi, opprinnelig beregning forklart.